Shyam A. Tailor, 6th April 2021

Tweet Follow @satailor96

Overview

Paper Link and Code & Pretrained Models

Graph neural networks (GNNs) have emerged as an effective way to build models over arbitrarily structured data. These approaches are commonly described in terms of the “message passing” paradigm (Gilmer et al. 2017) in which nodes send messages to each other to calculate the representation at the next layer. Although early work focused on semi-supervised learning on citation networks, more recent works have demonstrated that there are numerous possible application areas, including (but certainly not limited to):

1. Computer Vision: GNNs are often paired with the output of CNNs to aid in applications where high-level scene understanding is required. Examples include homography estimation (Sarlin et al. 2020), or activity recognition from videos (Zhang et al. 2020, Cheng et al. 2020).
2. Natural Language Processing: GNNs have been applied to tasks such as fake news detection and automated fact verification.
3. Code Analysis: Early work by Allamanis et al. demonstrated that GNNs could be applied to problems such as predicting variable misuse: whether a developer used a variable that type-checks, but actually isn’t what they intended.
4. Point Clouds: Many state of the art techniques for point cloud analysis involve constructing graphs from point clouds, and applying GNN architectures (Qi et al. 2018, Wang et al. 2018).
5. Recommender Systems: Ying et al. described Pinterest’s recommendation system which achieved higher performance than traditional methods by taking advantage of the graph structure.

Inspired by these applications, we ask how we can make GNN architectures more efficient to enable larger problems to be studied, and to allow for these techniques to be deployed to more resource constrained devices. Our work specifically approaches this problem from the perspective of efficient architecture design, and is analogous to approaches like MobileNet in computer vision, or the numerous attempts to make more efficient Transformer models. It is the second in a series of works by our lab investigating efficient GNNs: we have previously investigated quantization for GNNs in a paper to appear at ICLR 21.

We address two issues at the same time: hardware efficiency, while also not sacrificing expressivity. We find a good balance between these two alternative goals, and achieve state of the art accuracy with an implementation that explicitly accounts for trends in accelerator design. Our results have interesting implications for the community, and imply that flexible architectures are not necessarily required to achieve the best results.

What Do We Mean By Efficiency?

When we talk about “efficiency” for neural networks, we are usually referring to concepts such as runtime memory consumption, inference latency, and model size. Ideally, we would like to minimize all three. In this work we originally set out to handle the first two problems, but inadvertently also discovered our approach is also more parameter-efficient than competing architectures.

Ideally, we would like our memory consumption to be proportional to the number of vertices (\(\mathcal{O}(V)\)): this is as good as we can do. A (very) popular architecture, GCN (Kipf and Welling 2017), can achieve this goal since messages between nodes do not have to be materialized explicitly: everything can be implemented using sparse matrix multiplication (SpMM), including the backwards pass. GCN has since been surpassed accuracy-wise by other approaches, with the best performing architectures relying on explicit message construction between nodes; examples using this approach include GAT (Velickovic et al. 2018), MPNNs (Gilmer et al. 2017), and the recently proposed PNA model (Corso et al. 2020). These techniques enable a form of anisotropy as the messages are now a function of both the source and target nodes’ representations.

The Hardware Big Picture

While these approaches do boost accuracy, they have highly undesirable properties from a hardware perspective. They have memory consumption proportional to the number of edges (\(\mathcal{O}(E)\)) because of explicit message materialization. And while you may be able to fuse your message and aggregation operations at inference time in some cases, this is not an ideal situation, as it implies a complicated accelerator design. As Amdahl’s Law tells us, this is to be avoided where possible as we can get better results in terms of energy, latency and silicon area by optimizing for the common case.

Even ignoring the reality imposed by Amdahl’s Law, there is also the big picture to consider: given the great success of pruning in other areas of deep learning, we expect that there will be in-built support for SpMM in upcoming accelerators. We are already beginning to see this with Nvidia’s limited support for sparsity in the A100 tensor cores; the ARMv9 roadmap also specifically calls out sparsity support. This reason, among many others, is why we believe that targeting SpMM is the most plausible way to ensure that we see improvements in training and inference latency in the real world, and not just on paper¹.

How Can You Have Vertex-Wise Adaptation Without Message Materialization?

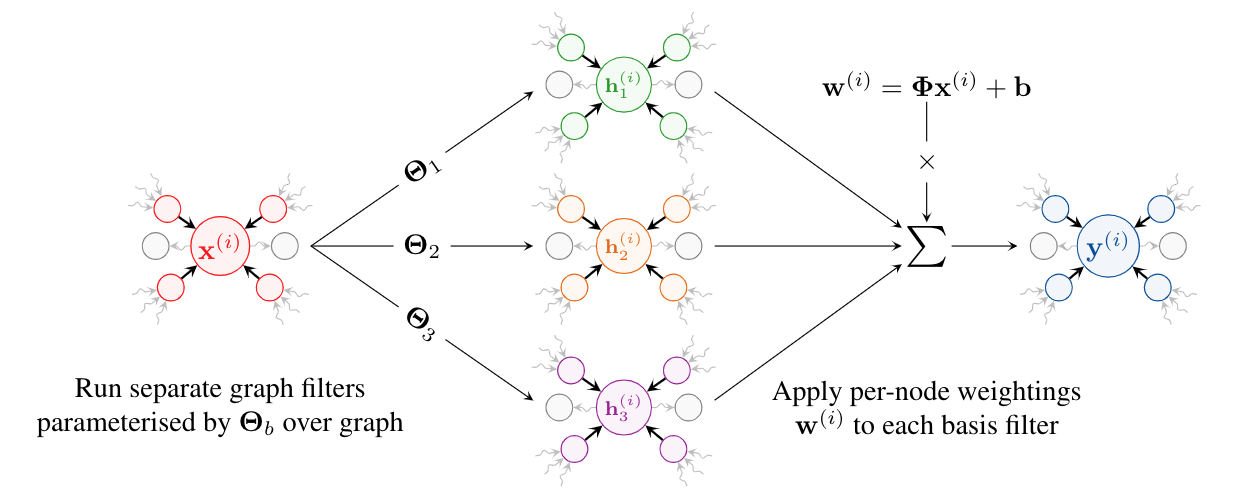
The core of our work is centered around the concept of adaptive filters. Our approach involves using a set of basis filters, and creating linear combinations of them at each node. We use symmetric normalization, which is justified in the paper, to obtain our EGC-S layer:

\[\mathbf{w}^{(i)} = \mathbf{\Phi} \mathbf{x}^{(i)} + \mathbf{b}\] \[\mathbf{y}^{(i)} = {\LARGE \|}_{h=1}^H \sum_{b = 1}^B w_{h,b}^{(i)} \; \sum_{j \in \mathcal{N}(i) \cup \{i\}} \quad\frac{1}{\sqrt{\text{deg}(i)\text{deg}(j)}} \mathbf{\Theta}_b \mathbf{x}^{(j)}\]

The simplest interpretation of this approach is that we have effectively given each vertex its own weight matrix: you can spot this by factorising out the \(\mathbf{\Theta}_b\) term. This enables us to have some kind of adaptivity at the granularity of vertices. This approach can be implemented using SpMM and requires only \(\mathcal{O}(V)\) memory when training–fulfilling our original motivation. To the best of our knowledge, this approach has not been applied in the modern neural network literature.

Our approach is directly inspired by my experience applying digital signal processing techniques in highly resource constrained scenarios—my background is in mobile & wearable technology. Our method is a technique for cheaply computing adaptive signal filters, and is not related to attention from an implementation perspective, although the end result obtained is similar. Adaptive filters are useful when the noise or signal characteristics vary with time or space, and are widely applied in applications such as noise cancellation. Of course, you can also view attention mechanisms through the “adaptive filtering” lens: this is easiest to see in Transformers (Vaswani et al. 2017). Attention in Transformers effectively involves calculating a convolutional filter dynamically at each node. One work proposing an alternative to a Transformer even explicitly predicts what the convolutional filter should be based on the local node representation, with no noticeable decrease in accuracy (Wu et al. 2019). We have effectively taken a different route to a similar end result, motivated by efficiency concerns. In practice, our approach does not seem detrimental on any of the 5 large real-world datasets we evaluated on—in fact, it seems to be better for graphs.

It’s worth noting that we don’t apply a softmax transformation to our combination coefficients. We did experiment with this, and we discovered that it actually harmed performance. One possible explanation is that by applying a softmax transformation to our combination coefficients we are effectively constraining each weight in the resulting combined matrix to a hyperplane. An alternative explanation is rooted in numerical issues: you can sometimes see this with GAT, where a small number of seeds perform badly just due to an unlucky initialization resulting in a vanishing gradient. Regardless, it’s worth pointing out that avoiding softmax is a good idea anyway when we’re deploying quantized models: softmaxed coefficients are tricky to quantize, therefore necessitating the shuffling of data between integer and floating point representations.

We find that this EGC-S variant is highly competitive with approaches such as GAT or MPNN based on our experiments on 5 varied and challenging graph datasets. There is no experiment where GAT outperforms EGC-S. We find that MPNN can sometimes outperform EGC-S when using a different aggregator, max, which provides stronger inductive biases for certain tasks.

SOTA Accuracy With Little Latency Overhead Through Aggregator Fusion

Inspired by the work on PNA, we can also integrate multiple aggregation functions, such as addition, maximum, standard deviation and others into our model, resulting in the EGC-M variant defined using generalised aggregation functions \(\oplus\). Perhaps surprisingly, we find that this minor modification is sufficient to obtain state of the art performance, often beating PNA by large margins. We did not find it necessary to search over multiple aggregator choices, with the limited choices assessed yielding roughly similar results. We note that it may be possible to obtain better results than we report through a larger grid search, or through automated techniques (NAS).

At first glance it would seem that we have to trade a large increase in latency to obtain improved accuracy. However, by paying attention to hardware implementation we can discover that this is false in many cases. The key observation is that sparse operations are memory-bound: most of the latency is not due to computation, but because we spend a lot of time waiting for data to arrive from memory. This is a pretty well understood phenomenon: unstructured sparsity results in difficult to optimize memory access patterns. We confirmed this observation by profiling SpMM on a GTX 1080Ti, and discovered that the overwhelming reason for instruction issue stalls was due to unmet memory dependencies. We propose aggregator fusion as a result of this observation. The technique essentially boils down to applying all aggregators to items that have arrived from memory, rather than fetching them multiple times. It is worth noting that this observation has implications for energy efficiency, in addition to the latency benefits: data movement is one of the largest drivers of energy consumption. According to a 2014 paper (Horowitz 2014), a 32-bit floating point add costs 0.9pJ, but the cost of the corresponding DRAM read is 640pJ—and the situation has likely become more extreme since then. Aggregator fusion eliminates multiple fetches, thereby significantly reducing data movement.

Closing Thoughts

We have proposed EGC, a new GNN architecture that achieves state of the art performance while also extensively accommodating hardware considerations. Our approach delivers greater memory efficiency, lower latency, and higher accuracy than competing approaches by incorporating adaptive filters and aggregator fusion. In the future, we hope to extend our work to enable features applying to edges to be efficiently used.

Our paper is on Arxiv, and code and pre-trained models for our work can be found on GitHub. Please feel welcome to contact us if you have any thoughts or questions.

Citing This Work

@misc{tailor2021adaptive,
      title={Adaptive Filters and Aggregator Fusion for Efficient Graph Convolutions}, 
      author={Shyam A. Tailor and Felix L. Opolka and Pietro Liò and Nicholas D. Lane},
      year={2021},
      eprint={2104.01481},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      note={GNNSys Workshop, MLSys '21 and HAET Workshop, ICLR '21}
}

Acknowledgements

This work was supported by Samsung AI and by the UK’s Engineering and Physical Sciences Research Council (EPSRC) with grants EP/M50659X/1 and EP/S001530/1 (the MOA project) and the European Research Council via the REDIAL project (Grant Agreement ID: 805194). FLO acknowledges funding from the Huawei Studentship at the Department of Computer Science and Technology of the University of Cambridge.

The authors would like to thank Ben Day, Javier Fernandez-Marques, Chaitanya Joshi, Titouan Parcollet and the anonymous reviewers who have provided comments on earlier versions of this work.

Footnotes

1. In addition, the vast majority of works proposing GNN accelerators focus on accelerating GCN, and not arbitrary GNNs; our approach can re-use this hardware. It remains an open research question to design accelerators that can handle a wide variety of sparsity levels, which is desirable if we intend to run arbitrary graph tasks and other deep learning workloads on the same silicon. ↩